How to Prove It - Solutions

Summary

• We can see a correspondence between set operations and statements. $A$ is the truth set of $P(x)$ and $B$ is the truth set of $Q(x)$ then
  • Truth set of $P(x) \land Q(x)$ is $A \cap B$.
  • Truth set of $P(x) \lor Q(x)$ is $A \cup B$.
  • Truth set of $\lnot P(x)$ is $U \setminus A$.

• Using logical forms of the statement, identities corresponding to set can be derived. For eg: $A \cup (B \cap C)$ is equivalent to $( A \cup B ) \cap (A \cup C)$ can be proved as:
  $A \cup (B \cap C) = x \in A \cup (B \cap C)$
  $\quad = x \in A \lor (x \in B \land x \in C)$
  Using distributive law,
  $\quad = (x \in A \lor x \in B) \land ( x \in A \lor x \in C)$
  Using definition of $\cup$
  $\quad = x \in (A \cup B) \land x \in (A \cup C)$
  Using definition of $\cup$
  $\quad = x \in ((A \cup B) \cap (A \cup C))$
  $\quad = ((A \cup B) \cap (A \cup C))$

  The above identity is similar to distributive law.

• $(A \cup B) \setminus (A \cap B) = (A \setminus B) \cup (A \setminus B)$. This can also be proved similarly as above.
• Set identities can also be proved using venn diagrams. One more way to prove them is by using truth tables also.
• Sets $A$ and $B$ are disjoint $iff\;A \cap B = \phi$.

Solutions

Soln1

(a) $A \cap B = \{3, 12\}$.

(b) $(A \cup B) \setminus C = \{1, 12, 20, 35\}$.

(c) $A \cup (B \setminus C) = \{1, 3, 12, 20, 35\}$.

No sets from above are disjoint. Set (a) and (b) both are subsets of (c).

Soln2

(a) $A \cup B = \{$ United States, Germany, China, Australia, France, India, Brazil $\}$.

(b) $(A \cap B) \setminus C = \phi$.

(c) $(B \cap C) \setminus A = \{\text{France}\}$.

We can see from above (c) is subset of (a). Also (b), (a) and (b), (c) are disjoint sets.

Soln3

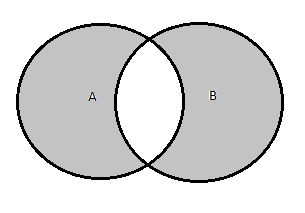
It can be easily seen that both $(A ∪ B)\setminus(A \cap B)\text{ and }(A \setminus B) \cup (B \setminus A)$ covers the same region.

Soln4

(a)

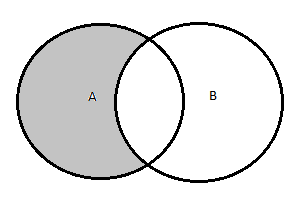
This can be verified easily from above diagram that $A \setminus (A \cap B) = A \setminus B$.

(b)

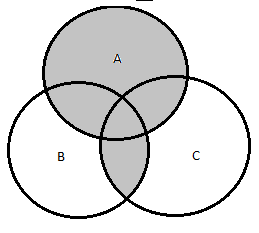
This can be verified easily from above diagram that $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$.

Soln5

Proof for first part(soln4a):

$A \setminus (A \cap B)$ is equivalent to:
$\quad= x \in A \land \lnot(x \in A \land x \in B)$
Using Demorgan’s Law,
$\quad= x \in A \land (x \notin A \lor x \notin B)$
Using Distribution Law,
$\quad= (x \in A \land x \notin A) \lor (x \in A \land x \notin B)$
As $(x \in A \land x \notin A)$ is a contradiction,
$\quad= (x \in A \land x \notin B)$
Using definition of set minus,
$\quad= (x \in A \setminus B)$
$\quad= (A \setminus B)$ Hence proved.

Proof for second part(soln4b):

$A \cup (B \cap C) = x \in A \cup (B \cap C)$
$\quad = x \in A \lor (x \in B \land x \in C)$
Using Distributive Law,
$\quad = (x \in A \lor x \in B) \land ( x \in A \lor x \in C)$
Using definition of $\cup$
$\quad = x \in (A \cup B) \land x \in (A \cup C)$
Using definition of $\cap$
$\quad = x \in ((A \cup B) \cap (A \cup C))$
$\quad = ((A \cup B) \cap (A \cup C))$ Hence Proved.

Soln6

(a)

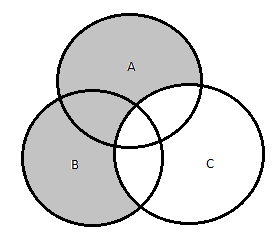
This can be verified from above diagram that $(A ∪ B) \setminus C = (A \setminus C) ∪ (B \setminus C)$.

(b)

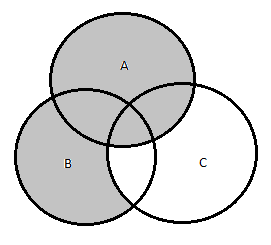
This can be verified from above diagram that $A ∪ (B \setminus C) = (A ∪ B) \setminus (C \setminus A)$.

Soln7

(a)
LHS:

$(A ∪ B) \setminus C = (x \in A \lor x \in B) \land x \notin C$
Using Distributive Law,
$\quad = (x \notin C \land x \in A) \lor (x \notin C \land x \in B)$
Using commutative law,
$\quad = (x \in A \land x \notin C) \lor (x \in B \land x \notin C)$
Using definition of $\setminus$
$\quad = (x \in (A \setminus C)) \lor (x \in (B \setminus C))$
Using definition of $\lor$
$\quad = x \in ((A \setminus C) \cup (B \setminus C))$

RHS:

$(A \setminus C) ∪ (B \setminus C) = (x \in A \land x \notin C) \lor (x \in B \land x \notin C)$
Using distributive law,
$\quad = ((x \in A \land x \notin C) \lor x \in B) \land ((x \in A \land x \notin C) \lor x \notin c)$
Using Absorption law,
$\quad = ((x \in A \land x \notin C) \lor x \in B) \land (x \notin C))$
Using Commutative law,
$\quad = (x \in B \lor (x \in A \land x \notin C)) \land (x \notin C))$
Using distributive law,
$\quad = ((x \in B \land x \notin C) \lor ((x \in A \land x \notin C) \land (x \notin C))$
Using associative law,
$\quad = ((x \in B \land x \notin C) \lor (x \in A \land (x \notin C \land x \notin C))$
Using Idempotent law,
$\quad = ((x \in B \land x \notin C) \lor (x \in A \land x \notin C))$
Using definition of $\setminus$
$\quad = x \in (B \setminus C) \lor (x \in (A \setminus C)$
Using definition of $\cup$
$\quad = x \in (B \setminus C) \cup (A \setminus C)$

From above we can see that after simplification LHS and RHS are same.

(b)

LHS:

$A ∪ (B \setminus C) = x \in A \lor (x \in B \land x \notin C)$
Using Distributive Law,
$\quad = (x \in A \lor x \in B) \land (x \in A \lor x \notin C)$
Using Double Negation law,
$\quad = (x \in A \lor x \in B) \land \lnot \lnot(x \in A \lor x \notin C)$
Using Demorgans Law,
$\quad = (x \in A \lor x \in B) \land \lnot(x \notin A \land x \in C))$
Using defn. of $\setminus$
$\quad = (x \in A \lor x \in B) \land \lnot(x \in (C \setminus A))$
Using defn. of $\cap$
$\quad = (x \in (A \cup B) \land \lnot(x \in (C \setminus A))$
Using defn. of $\setminus$
$\quad = x \in (A \cup B) \setminus (C \setminus A)$
$\quad = (A \cup B) \setminus (C \setminus A)$ = RHS. Hence Proved.

Soln8

(a)

$(A \setminus B) \setminus C = (x \in A \land x \notin B) \land x \notin C$
$\quad = x \in A \land x \notin B \land x \notin C$

(b)

$A \setminus (B \setminus C) = x \in A \land \lnot (x in B \land x \notin C)$
Using Demorgans Law,
$\quad = x \in A \land (x \notin B \lor x \in C)$
Using Demorgans Law,
$\quad = (x \in A \land x \notin B) \lor (x \in A \land x \in C)$
$\quad = x \in (A \setminus B) \lor (x \in (A \land C))$
$\quad = x \in ((A \setminus B) \cup (A \cap C))$

(c)

$(A \setminus B) ∪ (A ∩ C) = x \in (A \setminus B) \cup (A \cap C)$.

(d)

$(A \setminus B) \cup (A \setminus C) = (x \in A \land x \notin B) \land (x \in A \land x \notin C)$
$\quad = ((x \in A \land x \notin B) \land x \in A) \land ((x \in A \land x \notin B) \land x \notin C)$
$\quad = (x \in A \land x \notin B) \land ((x \in A \land x \notin B) \land x \notin C)$
$\quad = (x \in A \land x \notin B) \land x \notin C$
$\quad = x \in A \land x \notin B \land x \notin C$

(e)

$A \setminus (B \cup C) = x \in A \land \lnot(x \in B \lor x \in C)$
$\quad = x \in A \land (x \notin B \land x \notin C)$
$\quad = x \in A \land x \notin B \land x \notin C$

As can be seen above a, d and e are equivalent. Also b, and c are equivalent.

Soln9

1. $A = \{1, 2, 3, 4\}$, $B = \{3, 4, 5, 6\}$ then $(A \cup B) \setminus B = \{1, 2\}$.

2. $A = \{john, peter, amit, goldsmith\}$, $B = \{goldsmith, joshua\}$ then $(A \cup B) \setminus B = \{john, peter, amit\}$.

Soln10

(a) In the venn diagram given, there is no region corresponding to $(A \cap D) \setminus (B \cup C)$.

(b) First draw venn diagram for A, B and C using circles. Then draw a curve for D such that there is a region for every possible set that have possibility to contain some elements.

Soln11

(a)

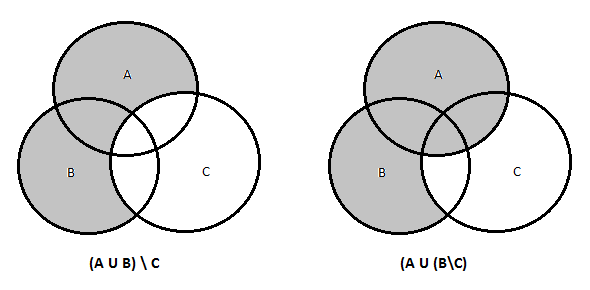
It can be seen from above diagram that $(A ∪ B)\setminus C \subseteq A ∪ (B \setminus C)$.

(b)

Let $A=\{1,2,3\}, B=\{1,4,5\}, C=\{1,4,6\}$.

$(A ∪ B)\setminus C = \{2, 3, 5\}$.

$A ∪ (B \setminus C) = \{1, 2, 3, 5\}$.

Soln12

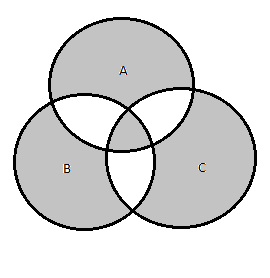
It can be verified that both $A \triangle (B \triangle C)$, and $(A \triangle B) \triangle C$ are equivalent as they corresponds to same region.

Soln13

For simplicity, I shall be using $A,\,B\,and\,C$ as logical statements corresponding to $x \in A, x \in B, x \in C$.

(a)

RHS:

$(A \cup C) \triangle (B \setminus C)$
$\quad = ((A \lor C) \lor (B \land \lnot C)) \land \lnot ((A \lor C) \land (B \land \lnot C))$
$\quad = ((A \lor C) \lor (B \land \lnot C)) \land (\lnot(A \lor C) \lor \lnot(B \land \lnot C))$
$\quad = ((A \lor C) \lor (B \land \lnot C)) \land ((\lnot A \land \lnot C) \lor (\lnot B \lor C))$
$\quad = (((A \lor C) \lor B) \land ((A \lor C) \lor \lnot C)) \land (((\lnot A \land \lnot C) \lor \lnot B) \lor ((\lnot A \land \lnot C) \lor C)))$
$\quad = ((A \lor C \lor B) \land (A \lor C \lor \lnot C)) \land (((\lnot A \lor \lnot B) \land (\lnot C \lor \lnot B)) \lor ((\lnot A \lor C) \land (\lnot C \lor C)))$
$\quad = ((A \lor C \lor B) \land true) \land (((\lnot A \lor \lnot B) \land (\lnot C \lor \lnot B)) \lor ((\lnot A \lor C) \land true))$
$\quad = (A \lor C \lor B) \land (((\lnot A \lor \lnot B) \land (\lnot C \lor \lnot B)) \lor (\lnot A \lor C))$
$\quad = (A \lor C \lor B) \land ((((\lnot A \lor \lnot B) \land \lnot C) \lor ((\lnot A \lor \lnot B) \land \lnot B)) \lor (\lnot A \lor C))$
$\quad = (A \lor C \lor B) \land ((((\lnot A \lor \lnot B) \land \lnot C) \lor \lnot B) \lor (\lnot A \lor C))$
$\quad = (A \lor C \lor B) \land (((\lnot A \lor \lnot B) \land \lnot C) \lor \lnot B \lor \lnot A \lor C)$
$\quad = (A \lor C \lor B) \land ((((\lnot A \lor \lnot B) \land \lnot C) \lor (\lnot B \lor \lnot A)) \lor C)$
$\quad = (A \lor C \lor B) \land ((\lnot B \lor \lnot A) \lor C)$
$\quad = ((A \lor B) \lor C) \land ((\lnot A \lor \lnot B) \lor C)$
$\quad = ((A \lor B) \land (\lnot A \lor \lnot B)) \lor C$
$\quad = ((A \lor B) \land \lnot( A \land B)) \lor C$
$\quad = (A \triangle B) \cup C$ = LHS.

(b)

RHS:

$(A \cap C) \triangle (B \cap C)$
$\quad = ((A \land C) \lor (B \land C)) \land \lnot ((A \land C) \land (B \land C))$
$\quad = ((A \land C) \lor (B \land C)) \land (\lnot (A \land C) \lor \lnot(B \land C))$
$\quad = ((A \land C) \lor (B \land C)) \land ( (\lnot A \lor \lnot C) \lor (\lnot B \lor \lnot C))$
$\quad = ((A \lor B) \land C) \land ( (\lnot A \lor \lnot B \lor \lnot C))$
$\quad = ((A \lor B) \land C) \land ( \lnot A \lor \lnot B \lor \lnot C)$
$\quad = (A \lor B) \land C \land ( \lnot A \lor \lnot B \lor \lnot C)$
$\quad = (A \lor B) \land (C \land (\lnot A \lor \lnot B \lor \lnot C))$
$\quad = (A \lor B) \land ((C \land (\lnot A \lor \lnot B)) \lor (C \land \lnot C))$
$\quad = (A \lor B) \land (C \land (\lnot A \lor \lnot B))$
$\quad = (A \lor B) \land (\lnot A \lor \lnot B) \land C$
$\quad = (A \lor B) \land \lnot ( A \land B) \land C$
$\quad = (A \triangle B) \cap C$ = LHS.

(c)

RHS:

$(A \setminus C) \triangle (B \setminus C)$
$\quad = ((A \land \lnot C) \lor (B \land \lnot C)) \land \lnot((A \land \lnot C) \land (B \land \lnot C))$
$\quad = ((A \lor B) \land \lnot C) \land \lnot(A \land \lnot C \land B \land \lnot C)$
$\quad = ((A \lor B) \land \lnot C) \land \lnot(A \land B \land \lnot C)$
$\quad = ((A \lor B) \land \lnot C) \land \lnot((A \land B) \land \lnot C)$
$\quad = ((A \lor B) \land \lnot C) \land (\lnot(A \land B) \lor \lnot \lnot C)$
$\quad = (A \lor B) \land \lnot C \land (\lnot(A \land B) \lor C)$
$\quad = (A \lor B) \land (\lnot(A \land B) \lor C) \land \lnot C$
$\quad = (A \lor B) \land ((\lnot(A \land B) \land \lnot C)\lor (C \land \lnot C))$
$\quad = (A \lor B) \land (\lnot(A \land B) \land \lnot C)$
$\quad = ((A \lor B) \land \lnot(A \land B)) \land \lnot C$
$\quad = (A \triangle B) \setminus C$ = LHS.

Skipping 14 and 15 as they are similar to 13.